Insertions And Shifting Algorithm

Introduction

The array insertion and shifting algorithm in Java is a fundamental technique for inserting an element into an array at a specific position while efficiently shifting the existing elements to accommodate the new addition.

This algorithm is essential for dynamically modifying the contents of an array and maintaining its integrity.

By leveraging this algorithm, developers can easily handle array insertions, ensuring optimal performance and maintaining the order of elements.

In this article, we will explore the implementation of the array insertion and shifting algorithm in Java, providing a step-by-step guide and a code example that demonstrates how to incorporate new elements into an array at desired positions seamlessly.

Insertion algorithms

Inserting an element at the start/middle of an array falls under array weaknesses, which might impact the performance if we are dealing with a massive array of elements as we need to shift the rest of the elements, which takes O(N) time unless we add new values at the end of the array, taking O(1) time. 

For example, consider an array of Characters { A, B, D, E, F } with indexes ranging from 0 to 4, and the length of the array being 5.

What happens if we insert a character C at index 2? or what happens we insert the character C at the last index?

We are inserting an element and not updating the index. Hence we need to shift the rest of the elements to make space for char C to insert it right index. Let us see both algorithms in practice. There are two insert positions we need to consider:

1. Inserting at the end.
2. Inserting at the start/middle.

1. Insert the item at the end

As explained in the "Overview of arrays" lesson. When we declare an array, we create an array containing all zeros.

// array of elements with capacity as 5
int[] values = new int[5]; // equivalent to `values = {0, 0, 0, 0, 0}`

All array values are defaulted to 0.

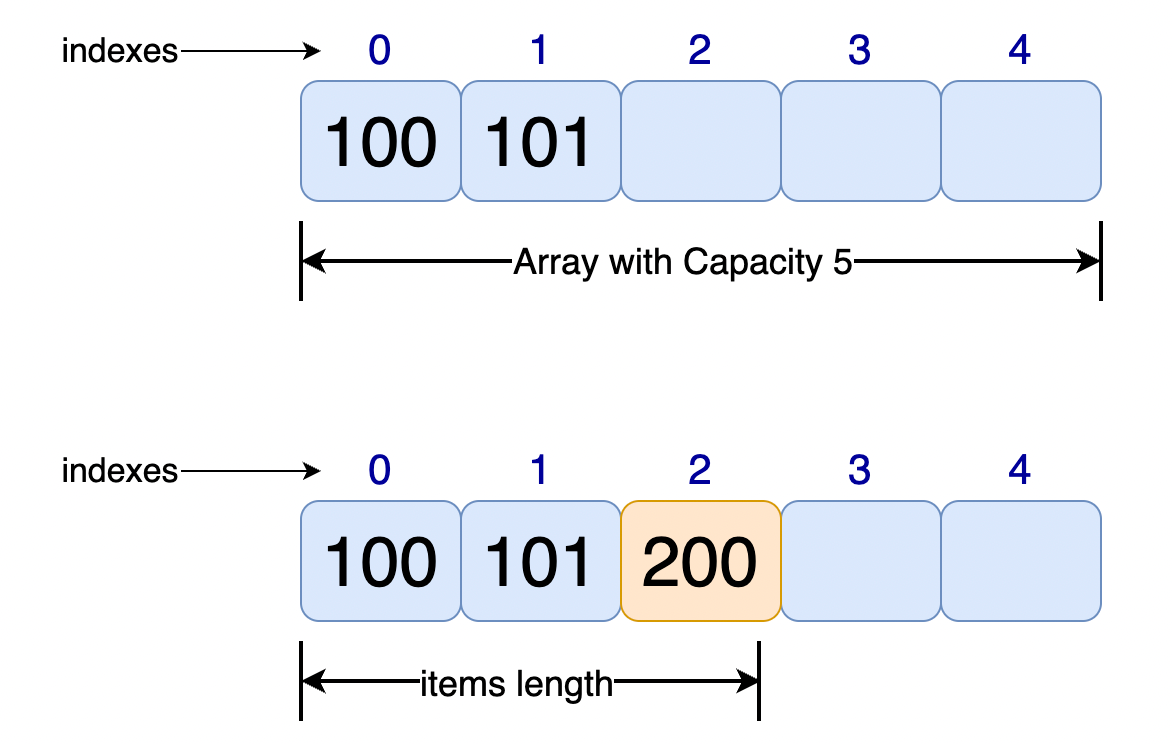
Let us use a variable currentLength to track the current items inserted in the array. Where currentLength points to the array's next index at any given time.

We use a simple snippet to insert elements into the array. We have inserted a value 200 at the end of the array(array length).

Illustration

The sketch looks like this:

Code

Enough talk. Here is a simple algorithm that creates an array with a size 5, and inserts 100, 101 values into the array. Finally, we insert an element at the array length.

package dev.ggorantala;

import java.util.Arrays;

public class ArrayAppends {
    public static void main(String[] args) {
        int[] A = new int[5];
        int currentArrayLength = 0;

        // Let us add 2 elements to the array
        for (int i = 0; i < 2; i++) {
            A[i] = i + 100;
            currentArrayLength++; // when i=1, length is set to 2
        }

        System.out.println(Arrays.toString(A)); // [100, 101, 0, 0, 0]
        System.out.println("current array length " + currentArrayLength); // 2
        System.out.println("Array capacity " + A.length); // 5
        System.out.println("Element insert at the end " + Arrays.toString(
            insertAtEnd(A, currentArrayLength))); // [100, 101, 200, 0, 0]
    }

    // Inserting an element at the end
    public static int[] insertAtEnd(int[] A, int currentArrayLength) {
        A[currentArrayLength] = 200;
        return A;
    }
}

/* 
Outputs:
[100, 101, 0, 0, 0]
current array length 2
Array capacity 5
Element insert at the end [100, 101, 200, 0, 0]
*/

You have seen adding elements at the end of an array. Let us see how we refactor our previous algorithm to insert values at the start or the middle.

Complexity Analysis

1. Time complexity: O(1), as we insert the value at the end.
2. Space complexity: O(1), no extra space is occupied other than the input memory.

2. Insert at the Start/Middle of the array

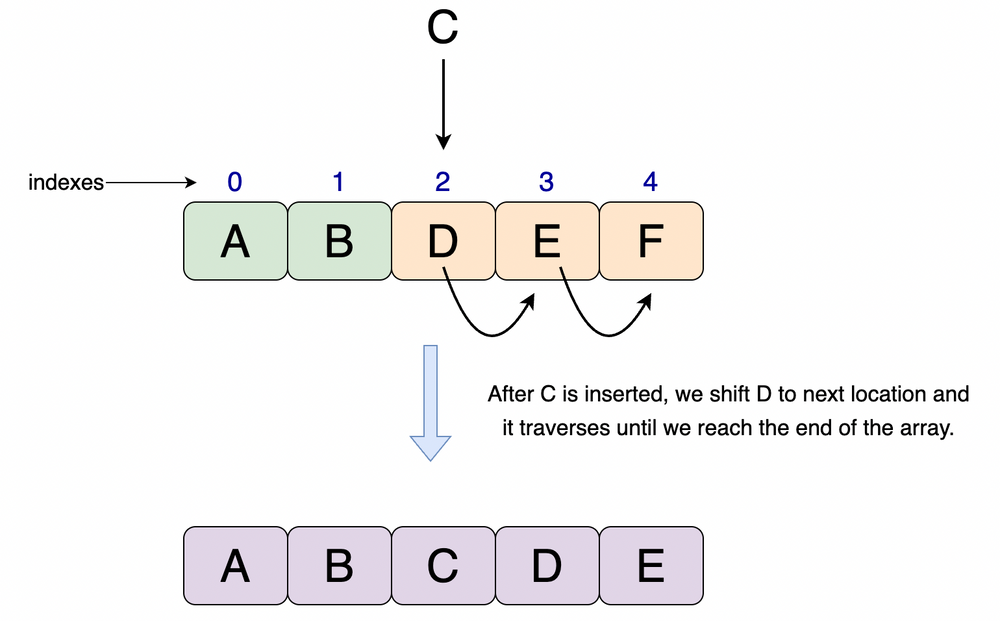
Think of a scenario where our array is filled with values. And we want to insert an item(not update) at the start/middle of the array.

Example

For example, consider an array A[10] that has elements {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} stored in it, and the array is full.

The array capacity/length and size are both equal to 10. (array capacity is calculated using A.length, but the items inserted in the array are how size is calculated).

At any given index less than the size of the array. If we want to insert data, we must first shift all the elements from that index to the right and then insert this new data.

Illustration

Code

import java.util.Arrays;

public class ArrayInsertsAtEnd {

  public static void main(String[] args) {
    int[] values = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
    int insertValue = 100;
    int insertAtIndex = 5;
    int i;

    System.out.println(Arrays.toString(values)); // [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]

    for (i = values.length - 2; i >= insertAtIndex; i--) {
      values[i + 1] = values[i];
    }

    values[insertAtIndex] = insertValue;

    System.out.println(Arrays.toString(values)); // [1, 2, 3, 4, 5, 100, 6, 7, 8, 9]
  }
}

Complexity Analysis

1. Time complexity: O(N), as we shifted elements from the insert position to the right. In the worst case, we insert an element at the zeroth index and shift all elements to the right. This is the reason we consider the time as O(N).
2. Space complexity: O(1), no extra space is occupied other than the input memory.

We discussed array capacity vs length and learned about inserting an element into the array at the start, middle, and end. We also learned how to shift array elements to make space for the new item to be inserted.

I hope these lessons and examples on shifting algorithms help you gain some ideas and tricks for solving coding questions at LeetCode, HackerRank, CodeChef, etc., to ace top tech companies and fast-paced startups.