Monotonic Array

Introduction

A monotonic array is an array that is either increasing or monotonic decreasing.

Problem Statement

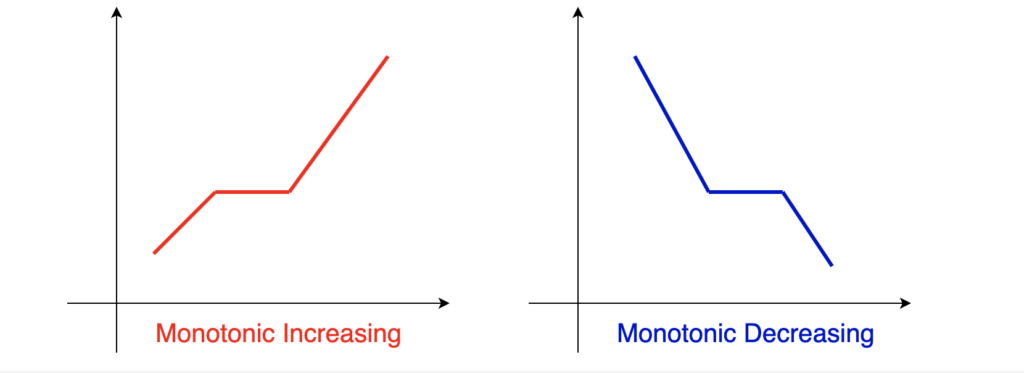
An array A is monotone increasing(📈) if for all i <= j, A[i] <= A[j], where i and j are index elements.

An array A is monotone decreasing (📉) if for all i >= j, A[i] >= A[j]. true is returned if and only if the given array A is monotonic.

Explanation:

Monotone increasing: An array A is called monotone increasing if the first number is less than or equal to the second number, the second number is less than or equal to the third number, and so on, and vice versa.

Monotone decreasing: An array A is called monotone decreasing if the first number is greater than or equal to the second number, the second number is greater than or equal to the third number, and so on, and vice versa.

Test case #1

  Input: [1, 2, 2, 3]  
  
  Output: true

Test case #2

  Input: [1, 2, 6, 2, 3]  
  
  Output: false

Test case #3

  Input: [7, 2, 1]  
  
  Output: true

Thought Process

An array is called monotonic if the index of each element increases from the first to the last or decreases from the first to the last.

Algorithm

We need to run two for loops to check if either of the loops returns true.

• We must check if the previous index is less than the current one for the monotonic increasing array.
• We must check if the previous index is greater than the current one for the monotonic decreasing array.

Finally, we return true if either of the loops evaluates to true.

Optimal way: we can do using one pass but let us look at both the algorithms.

Intuition

There are different ways to solve this problem, but the one that is simple yet powerful are:

1. Two-pass approach
2. One-pass approach

Two-pass approach

You need to run two loops to check if the elements are in increasing or decreasing order.

Code

class MonotonicArray {
  public static void main(String[] args) {
    int[] input = {1, 2, 2, 3};
    System.out.println(isMonotonic(input)); // true
  }

  public static boolean isMonotonic(int[] array) {
    return isIncreasing(array) || isDecreasing(array);
  }

  public static boolean isIncreasing(int[] nums) {
    for (int i = 1; i < nums.length; i++)
      if (nums[i - 1] > nums[i]) {
        return false;
      }
    return true;
  }

  public static boolean isDecreasing(int[] nums) {
    for (int i = 1; i < nums.length; i++)
      if (nums[i - 1] < nums[i]) {
        return false;
      }
    return true;
  }
}

Complexity Analysis

1. Time complexity: We have two for-loops running O(n) times each. So, the overall time complexity is O(n) + O(n) = 2*O(n). Hence, the time is O(n) for this algorithm.
2. Space complexity: O(1), no extra space is used for this algorithm.

Let us optimize the above code snippet with a single loop.

One-Pass approach

The above algorithm can be optimized to a single loop using boolean flags.

Code

class MonotonicArray {
  public static void main(String[] args) {
    int[] input = {1, 2, 2, 3};
    System.out.println(isMonotonic(input)); // true
  }

  public static boolean isMonotonic(int[] array) {
    boolean isIncreasing = true;
    boolean isDecreasing = true;

    for (int i = 1; i < array.length; i++) {
      if (array[i] < array[i - 1]) {
        isDecreasing = false;
      }

      if (array[i] > array[i - 1]) {
        isIncreasing = false;
      }
    }

    return isIncreasing || isDecreasing;
  }
}

Complexity Analysis

1. Time complexity: We have one for-loop running O(n) time. So, the overall time complexity is O(n) for this algorithm.
2. Space complexity: O(1), no extra space is used for this algorithm.