The Two Sum problem is a classic problem, and this has been listed first as one of the basic questions one has to solve when prepping for coding interviews. This is one of the most popular questions asked in such interviews.

Companies that have asked this in their coding interview are Facebook, Amazon, Apple, Netflix, Google, Microsoft, Adobe, and many more top tech companies.

Problem Statement

In the two-sum problem, given an array of integers, nums and an integer, return the indexes of the two numbers such that they add up to the target. You may assume that each input would have exactly one solution, and you may not use the same element twice.

You can return the answer in order.

Test case#1

Input: nums = [2, 7, 11, 15], target = 18

Output: [1, 2] or [2, 1] 
// (because nums[1] + nums[2] == 18, we return [1, 2])

Test case#2:

Input: nums = [3, 2, 4], target = 6

Output: [1, 2] or [2, 1]

Test case#3:

Input: nums = [3, 3], target = 6

Output: [0, 1] or [1, 0]

Illustration

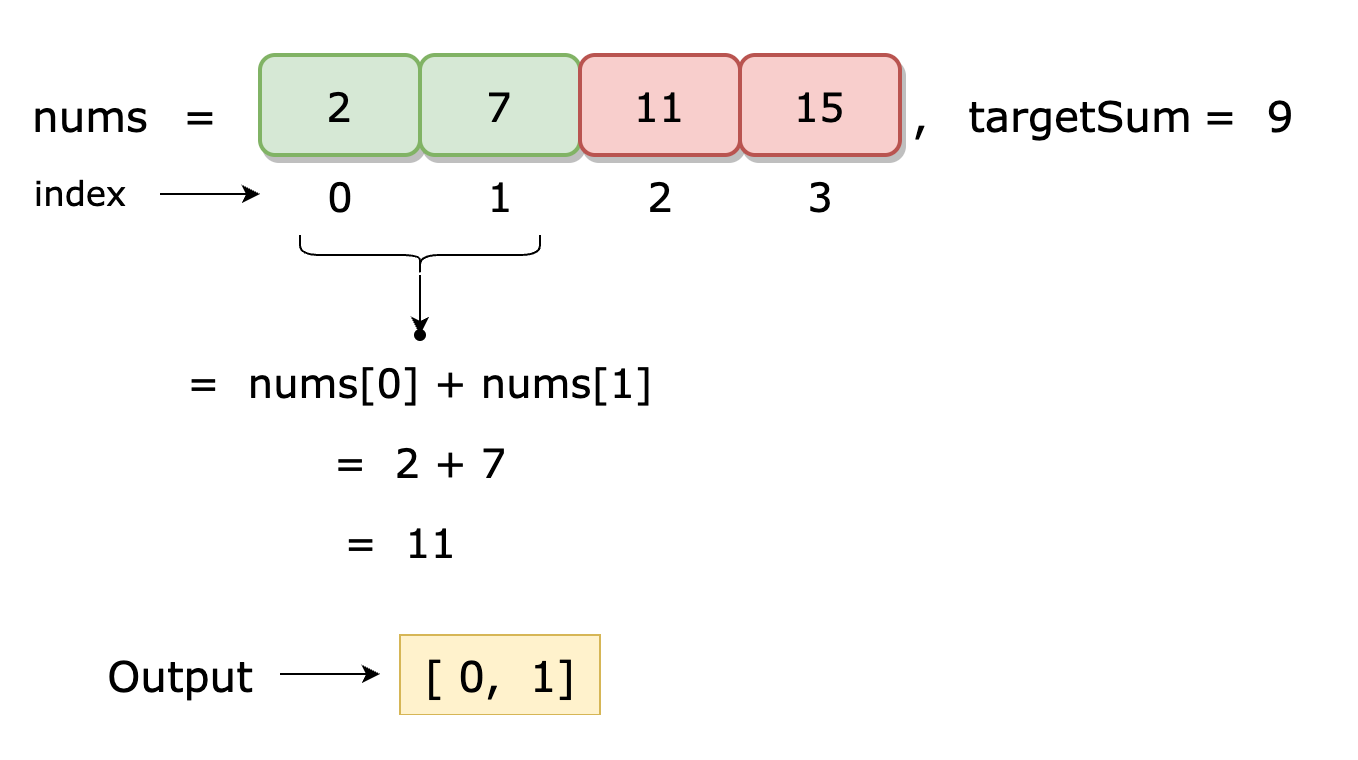
Thought process

My first thoughts when looking at this problem and the questions I have are:

1. Are we having duplicates in the array?
2. What if two pairs match the target ? Which pair should we return? Should we return both pairs?
3. What are the constraints? At least two elements should be present in the nums array.

Once the above questions are discussed with the interviewer, I will propose different solutions. The ones that come to my mind right now are

1. Brute force / Maths formula,
2. Hashing (key, value) approach,
   1. Two-pass
   2. One-pass

Approach 1: Naive / Math formula

Intuition

The brute force approach is simple. We need to loop through each element x and find another value that equals y. The question clearly states that two numbers add up to target.

So, the math formula becomes:

x + y = target

Algorithm

1. Initialize two nested loops to iterate through each pair of elements in the array.
   • Outer loop (i) ranges from 0 to the nums.length - 1.
   • The inner loop (j) ranges from i + 1 to the nums.length - 1.
2. Within the inner loop, check if the sum of elements at indices i and j equals the target.
   • If true, return a new array containing the indices [i, j] as they form a pair with the desired sum.
3. If no pair is found during the iterations, return a default array [-1, -1] to indicate that no such pair exists.

class Solution {
    public int[] twoSum(int[] nums, int target) {
        for (int i = 0; i < nums.length; i++) {
            for (int j = i + 1; j < nums.length; j++) {
                if (nums[j] + nums[i] == target) {
                    return new int[] { i, j };
                }
            }
        }
        return new int[] { -1, -1 };
    }
}
// outputs [1, 2]

Or, in simple terms, we can say we find x and y can be replaced with (target - x).

class Solution {
    public int[] twoSum(int[] nums, int target) {
        for (int i = 0; i < nums.length; i++) {
            for (int j = i + 1; j < nums.length; j++) {
                if (nums[j] == target - nums[i]) {
                    return new int[] { i, j };
                }
            }
        }
        return new int[] { -1, -1 };
    }
}
// outputs [1, 2]

Complexity analysis

1. Time complexity: O(n2), we try to find its complement by looping through the rest of the array, which takes O(n) time. Therefore, the time complexity is O(n2), where n is the length of the elements present in the array.
2. Space complexity: O(1), as no extra space is utilized.

Approach 2: Memoization [Accepted]

Intuition

To apply the same math formula from the above approach, we'll use a single for-loop instead of two for-loops. However, this will require extra space.

We will apply the same math formula from the above approach, but instead of having two for-loops, we use a single for-loop to achieve this. O(N) time and space instead O(n2) from previous naive approach.

If x is the value we are expecting, then target - x is the second element. Keeping this in mind the two elements are

x, (target - x)

So, when iterating the elements, you get X value and check if (10 - X) which is Y is present in the HashTable, isn’t that easy to find? also, this is a constant O(1) lookup time.

While iterating the array elements, check if the current element x is there a target - x element.

Algorithm

1. Initialize a HashMap (ans) to store the elements of the array and their corresponding indices.
2. Iterate through the array using a single loop.
   • For each element at index i, calculate the difference as target - nums[i].
3. Check if the calculated difference exists in the HashMap (ans).
   • If true, return a new array containing the indices [ans.get(difference), i] as they form a pair with the desired sum.
4. If the difference is not found in the HashMap, add the current element (nums[i]) and its index (i) to the HashMap.
5. If no pair is found during the iterations, return a default array [-1, -1] to indicate that no such pair exists.

The following solution uses HashMap.

class Solution {
    public int[] twoSum(int[] nums, int target) {
        Map<Integer, Integer> ans = new HashMap<>();

        for (int i = 0; i < nums.length; i += 1) {
            int difference = target - nums[i];

            if (ans.containsKey(difference)) {
                return new int[] { ans.get(difference), i };
            }
            ans.put(nums[i], i);
        }

        return new int[] { -1, -1 };
    }
}
// outputs [1, 2]

Complexity Analysis

Time complexity: O(n), we traverse the list containing n elements exactly twice. Since the hash table reduces the look-up time to O(1), the time complexity is O(n).

Space complexity: O(n), the extra space required depends on the number of items stored in the hash table, which stores n elements.